Monoclonal antibody disposition: a simplified PBPK model and its implications for the derivation and interpretation of classical compartment models

Abstract

The structure, interpretation and parameterization of classical compartment models as well as physiologically-based pharmacokinetic (PBPK) models for monoclonal antibody (mAb) disposition are very diverse, with no apparent consensus. In addition, there is a remarkable discrepancy between the simplicity of experimental plasma and tissue profiles and the complexity of published PBPK models. We present a simplified PBPK model based on an extravasation rate-limited tissue model with elimination potentially occurring from various tissues and plasma. Based on model reduction (lumping), we derive several classical compartment model structures that are consistent with the simplified PBPK model and experimental data. We show that a common interpretation of classical two-compartment models for mAb disposition—identifying the central compartment with the total plasma volume and the peripheral compartment with the interstitial space (or part of it)—is not consistent with current knowledge. Results are illustrated for the monoclonal antibodies 7E3 and T84.66 in mice.

Appendices

Appendix: The role of FcRn and endogenous IgG in PBPK models of mAb disposition

From saturable IgG–FcRn interaction to linear mAb clearance

We illustrate that under commonly encountered (dosing) conditions, the clearance of mAbs in the endosomal space can be expected to be linear, regardless of the level of saturation of FcRn that protect mAb from degradation.

Denoting by IgG_mAb and IgG_endo the therapeutic and endogenous IgG concentrations in the endosomal space of endothelial cells, the resulting total IgG concentration was given by

$${\rm IgG} = {\rm IgG}_{\rm endo} + {\rm IgG}_{\rm mAb}.$$

In the endosomal space, free IgG binds to free FcRn with a dissociation constant K _D forming an ${\rm IgG}\!:\!{\rm FcRn}$ complex. The relevance of FcRn stems from the fact that it protects IgG from catabolism [48]: While the complex is recycled to the interstitial and/or plasma space, free IgG is eventually catabolized in the lysosomes:

$$\begin{aligned} &{\rm IgG}_{\rm u} + {\rm FcRn}_{\rm u} \;\overset{\overset{K_{\rm D}}{\longrightarrow}}{\longleftarrow}\; {\rm IgG}_{\rm b} \longrightarrow \rm{recycling}\\ &{\rm IgG}_{\rm u} \;\overset{k_{\rm deg}}{\longrightarrow}\; {\rm catabolism} \end{aligned}$$

To study the IgG–mAb interaction in more detail, we denoted by FcRn_u free FcRn, and by IgG_u and IgG_b the free and FcRn-bound IgG. Consequently, IgG_u is the sum of the free endogenous and free therapeutic IgG. Two conservation relations IgG = IgG_u + IgG_b and FcRn = FcRn_u + IgG_b hold.

In the sequel, we made the assumption that the K _D values of IgG_endo and IgG_mAb are comparable. This is a reasonable assumption for most mAbs—however, it does not hold for mAbs specifically engineered for high binding affinity to FcRn.

Binding processes are typically fast compared to the time-scale of other pharmacokinetic processes. Assuming a quasi-steady state for FcRn binding yielded ${\rm IgG}_{\rm u} \cdot {\rm FcRn}_{\rm u} = K_{\rm D} \cdot {\rm IgG}_{\rm b}$. Solving for the bound concentration and exploiting the conservation relations yielded

$${\rm IgG}_{\rm b} = \frac{{\rm FcRn}_{\rm u}}{K_{\rm D} +{\rm FcRn}_{\rm u}} \cdot {\rm IgG}.$$

(30)

Exploiting again the second conservation relation, we obtained

$${\rm FcRn} = {\rm FcRn}_{\rm u} + \frac{{\rm FcRn}_{\rm u}}{K_{\rm D} + {\rm FcRn}_{\rm u}} \cdot {\rm IgG}$$

and finally

$${\rm FcRn}_{\rm u} = \frac{1}{2} \Big({\rm FcRn}_{\rm eff} + \sqrt{({\rm FcRn}_{\rm eff})^2 + 4K_{\rm D}\cdot {\rm FcRn}} \Big)$$

(31)

with FcRn_eff = (FcRn − IgG − K _D). This allowed us to determine the fraction unbound fu_IgG based on Eq. (30) as

$${\rm fu}_{\rm IgG} = \frac{{\rm IgG}_{\rm u}}{{\rm IgG}} = 1-\frac{{\rm IgG}_{\rm b}}{{\rm IgG}} = \frac{K_{\rm D}}{K_{\rm D} + {\rm FcRn}_{\rm u}}$$

(32)

with FcRn_u defined in Eq. (31). We defined the level of saturation of FcRn as

$${\rm FcRn \,saturation \,level} = \frac{{\rm FcRn}-{\rm FcRn}_{\rm u}}{{\rm FcRn}}.$$

Figure 7 (left) shows the FcRn-saturation level as a function of the total IgG concentration, expressed in terms of units of total FcRn. We clearly identified two regimes: (i) for IgG lower than FcRn, the saturation level of FcRn appears to be linearly increasing with increasing IgG concentration; (ii) for IgG larger than total FcRn, the FcRn-saturation level appears to be 1. As shown below in "Theoretical derivation of FcRn saturation level and fraction unbound of mAb" section, this behavior can be theoretically justified based on the reasonable assumption that K _D ≪ FcRn, i.e., that IgG has a very high affinity to FcRn. This assumption is in line with the physiological function of FcRn. For the mAb 7E3 in mice, we estimated the total FcRn concentration to be $2.2 \cdot 10^5$ nM, while K _D was reported to be 4.8 nM (see Table 1), thereby supporting the assumption K _D ≪ FcRn.

Fig. 7

FcRn saturation level (left) and fraction unbound of IgG (right) as a function of the total IgG concentration (stated in units of total FcRn). Due to the high affinity binding of IgG to FcRn, the FcRn saturation level growth practically linearly with IgG concentration, until FcRn is fully saturated. As a consequence, the fraction unbound fu_IgG of IgG is practically zero until IgG concentration exceeds total FcRn concentration, when it follows the form fu_IgG = 1 − FcRn/IgG. We choose FcRn = 10⁵ nM and K _D = 4.8 nM, in line with values reported in Table 1

As shown in Fig. 7 (right), the fraction unbound fu_IgG also exhibited two regimes: (i) a phase of IgG concentration below FcRn, where fu_IgG is almost zero, and (ii) a phase of hyperbolic increase for IgG above FcRn. This behavior can again be justified theoretically, as shown in the Appendix "Theoretical derivation of FcRn saturation level and fraction unbound of mAb" and summarized as

$${\rm fu}_{\rm IgG} = \left\{ \begin{array}{ll} 0; & {\rm IgG} \leq {\rm FcRn} \\ 1-\frac{{\rm FcRn}}{{\rm IgG}}; & {\rm IgG} > {\rm FcRn}\\ \end{array}\right.$$

Without the underlying theoretical justification, such a model was proposed in [4], termed the cutoff model, based on some cutoff value ‘MAX’ (that is identical to total FcRn).

The above derivations have direct impact on modeling endosomal clearance and the FcRn-mediated salvage mechanism for a large number of mAbs. If the total IgG concentration is dominated by endogenous IgG and hardly perturbed by the administration of therapeutic IgG, i.e, IgG_mAb ≪ IgG_endo, which implies IgG ≈ IgG_endo, then the fraction unbound of mAb is constant, i.e.,

$${\rm fu}_{\rm mAb} = {\rm fu}_{\rm IgG} \approx {\rm fu}_{{\rm IgG}_{\rm endo}} = {\rm const}.$$

(33)

Such a situation is quite common for many mAbs. In mice, the baseline concentration of endogenous plasma IgG1 is reported to be 14.7 μM in [26, 49]. In [4], the author showed that the administration of an i.v. bolus of 8 mg/kg therapeutic IgG (7E3) does not affect the overall endogenous plasma level of IgG. The same can be shown to hold true for many mAbs in human (see "Discussion" section). Under such conditions, the extent of saturation of FcRn and consequently the fraction unbound fu_mAb only depends on the endogenous IgG concentration; in other words, it is set by the endogenous IgG levels.

Theoretical derivation of FcRn saturation level and fraction unbound of mAb

The special form of the dependance of the

$${\rm FcRn\,saturation\,level} = 1-\frac{{\rm FcRn}_{\rm u}}{{\rm FcRn}}$$

(34)

on the total IgG concentration can be theoretically justified from Eq. (31). To this end, we introduced the parameters

$$\epsilon = \sqrt{\frac{K_{\rm D}}{{\rm FcRn}}} \quad{\rm and }\quad {\it x} = 1-\epsilon^2 - \frac{{\rm IgG}}{{\rm FcRn}}.$$

(35)

Due to very tight binding of endogenous IgG and mAb to FcRn, we made the reasonable assumption that $\epsilon$ is very small, i.e., $\epsilon\ll1$. For 7E3 in mice, we estimated $\epsilon<5\cdot10^{-3}$ from Table 1. Dividing in Eq. (31) both sides by FcRn yielded the fraction unbound of FcRn:

$$\frac{{\rm FcRn}_{\rm u}}{{\rm FcRn}} = \frac{1}{2} \left( 1-\epsilon^2 - \frac{{\rm IgG}}{{\rm FcRn}} + \sqrt{\left(1-\epsilon^2 - \frac{{\rm IgG}}{{\rm FcRn}}\right)^2 + 4\epsilon^2}\right),$$

(36)

or ${\rm FcRn}_{\rm u}/{\rm FcRn}=1/2\cdot(x+\sqrt{x^2+4\epsilon^2}).$ When ${\rm IgG}/{\rm FcRn}=(1-\epsilon)$, i.e., when (total) IgG concentration is approximately equal to the (total) FcRn concentration, it is x = 0 and therefore ${\rm FcRn}_{\rm u}/{\rm FcRn}=\epsilon$. Now, the larger the IgG concentration, the larger the bound fraction of FcRn and the smaller the unbound fraction of FcRn. Thus, ${\rm IgG}/{\rm FcRn}\geq(1-\epsilon)$ implies

$$\frac{{\rm FcRn}_{\rm u}}{{\rm FcRn}}\leq \epsilon.$$

(37)

This finally resulted in the lower bound on the FcRn saturation level:

$$\rm{FcRn\,saturation \,level} = 1-\frac{{\rm FcRn}_{\rm u}}{{\rm FcRn}} \geq 1-\epsilon$$

(38)

for ${\rm IgG}/{\rm FcRn}\geq(1-\epsilon)$. For the upper bound for small IgG concentrations with $\epsilon< x$, we used a simple estimate on the square-root term $\sqrt{x^2+4\epsilon^2} < \sqrt{x^2+4x\epsilon}$ and applied the Taylor expansion to first order

$$\sqrt{x^2+ 4\epsilon x} \;\dot{ = }\; x + 2\epsilon$$

(39)

for $x\gg \epsilon$. This resulted in

$$\frac{{\rm FcRn}_{\rm u}}{{\rm FcRn}} \leq 1-\epsilon^2-\frac{{\rm IgG}}{{\rm FcRn}} +\epsilon.$$

(40)

On the other hand, by simply neglecting the $4\epsilon^2$ term in the square root in Eq. (36), we obtained

$$1-\epsilon^2 - \frac{{\rm IgG}}{{\rm FcRn}} \leq \frac{{\rm FcRn}_{\rm u}}{{\rm FcRn}}.$$

(41)

From these two inequalities and Eq. (34) we finally obtained

$$\frac{{\rm IgG}}{{\rm FcRn}} -\epsilon\cdot(1-\epsilon) \leq \rm{FcRn \,saturation\, level} < \frac{{\rm IgG}}{{\rm FcRn}} + \epsilon^2$$

(42)

for $x\gg \epsilon,$ i.e., ${\rm IgG}/{\rm FcRn}\ll 1-\epsilon-\epsilon^2$. Taken together, Eqs. (38) and (42) theoretically justify the peculiar form of the FcRn-saturation level depicted in Fig. 7 (left).

The above derivation also allowed us to theoretically justify the dependence of the fraction unbound fu_IgG on IgG, as shown in Fig. 7 (right). For ${\rm IgG}/{\rm FcRn}=(1-\epsilon)$ it is ${\rm FcRn}_{\rm u}/{\rm FcRn}=\epsilon$ as before, and

$$\begin{aligned} {\rm fu}_{\rm IgG} =& \frac{K_{\rm D}}{K_{\rm D}+{\rm FcRn}_{\rm u}} = \frac{\epsilon^2}{\epsilon^2+{\rm FcRn}_{\rm u}/{\rm FcRn}} \\ =& \frac{\epsilon^2}{\epsilon^2+\epsilon} = \frac{\epsilon}{1+\epsilon} < \epsilon. \end{aligned}$$

(43)

Since fu_IgG decreases monotonically with decreasing IgG concentration, the bound ${\rm fu}_{\rm IgG}<\epsilon$ continues to hold for all ${\rm IgG}<(1-\epsilon){\rm FcRn}$. For larger IgG concentrations, we started from the relation

$$\begin{aligned} {\rm fu}_{\rm IgG} =& \frac{{\rm IgG}_{\rm u}}{{\rm IgG}} = \frac{{\rm IgG}-({\rm FcRn}-{\rm FcRn}_{\rm u})}{{\rm IgG}} \\ =& 1-\frac{{\rm FcRn}}{{\rm IgG}} + \frac{{\rm FcRn}_{\rm u}}{{\rm FcRn}}\cdot \frac{{\rm FcRn}}{{\rm IgG}}, \end{aligned}$$

(44)

where we exploited IgG_b = FcRn_b = FcRn − FcRn_u. For ${\rm IgG}/{\rm FcRn}\geq (1-\epsilon),$ we obtained with (37) the inequality

$$1-\frac{{\rm FcRn}}{{\rm IgG}} \leq {\rm fu}_{\rm IgG} < 1-\frac{{\rm FcRn}}{{\rm IgG}} +\epsilon \cdot (1-\epsilon),$$

(45)

where the first inequality trivially follows from Eq. (44). Taken together, Eqs. (43) and (45) theoretically justify the peculiar form of the fraction unbound of IgG depicted in Fig. 7 (right).

Step-wise reduction of a detailed PBPK model of mAb disposition

Eliminating the need of endogenous IgG

The starting point of our simplified model was the tissue model of mAb disposition presented in [7, Fig. 2]. The tissue model comprised the vascular, endosomal and interstitial sub-compartments with the corresponding volumes V _p, V _e and V _i. The following processes were considered: (i) transport into the interstitial space via convective transport through the paracellular pores in the endothelium (simplified two-pore model); (ii) convective transport via the lymph fluid from the interstitial space; (iii) uptake from the plasma and interstitial spaces into the endosomal compartments via fluid phase endocytosis; (iv) binding to FcRn in the endosomal compartments, (v) salvage of FcRn-bound complexes to the plasma and interstitial spaces; (vi) lysosomal degradation of the unbound species in the endosomal spaces. The corresponding system of differential equations for the rates of change of the (total) concentration in the vascular space C _p, in the endosomal space C _e and in the interstitial space C _i are given by

$$V_{\rm p} {\rm \frac{d}{dt}}{C_{\rm p}} = Q \cdot C_{\rm in} - (Q-L) \cdot C_{\rm p} - L (1-{\rm \sigma_{\rm vas}}) C_{\rm p}- V_{\rm p} k_{\rm in} \cdot C_{\rm p} + {\rm FR} \cdot V_{\rm e} k_{\rm out} (1-{\rm fu}) C_{\rm e}$$

(46)

$$V_{\rm e} {\rm \frac{d}{dt}}{C_{\rm e}} = V_{\rm p} k_{\rm in} \cdot C_{\rm p} + V_{\rm i} k_{\rm in} \cdot C_{\rm i} - V_{\rm e} k_{\rm out} (1-{\rm fu})\cdot C_{\rm e}-{\rm CL}_{\rm e} \cdot {\rm fu} \cdot C_{\rm e}$$

(47)

$$V_{\rm i} {\rm \frac{d}{dt}}{C_{\rm i}} = L(1-{\rm \sigma_{\rm vas}})C_{\rm p} - L(1-{\rm \sigma_{\rm lymph}}) C_{\rm i} - V_{\rm i} k_{\rm in}\cdot C_{\rm i}+ (1-{\rm FR}) \cdot V_{\rm e} k_{\rm out} (1-{\rm fu})\cdot C_{\rm e},$$

(48)

with the parameters having the following meaning: Q and L denoted the plasma and lymph flows, ${\rm \sigma_{\rm vas}}$ and ${\rm \sigma_{\rm lymph}}$ denoted the vascular and lymphatic reflection coefficients, k _in denoted the endosomal uptake rate constant, k _out denoted the recirculation rate constant, and FR denoted the recirculation fraction of bound antibody from the endosomal into the vascular space. The unbound antibody in the endosomal space was subject to elimination following a linear clearance denoted by CL_e. The fraction unbound fu in the endosome was defined as in Eq. (32).

The authors in [7] explicitly considered endogenous IgG in their model—in addition to therapeutic IgG to account for the competition for binding of mAb and endogenous IgG to FcRn. Based on the observation preceding Eq. (33) and thereon based derivations, we could greatly simplify the above tissue model by only implicitly considering endogenous IgG. We indeed assumed that the fraction unbound of mAb in the endosome is constant. Therefore, we defined the total FcRn-mediated export flow and the endosomal intrinsic clearance as

$$Q_{\rm out} = V_{\rm e} k_{\rm out} \cdot (1-{\rm fu})$$

(49)

$${\rm CLint}_{\rm e} = {\rm CL}_{\rm e} \cdot {\rm fu}.$$

(50)

This was the basis for an intermediate complexcity of a PBPK model for mAbs disposition.

An intermediate complexity of PBPK models for mAb disposition

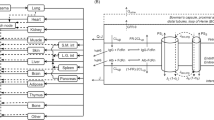
The intermediate PBPK model comprised 32 compartments representing the most relevant anatomical spaces involved in mAb disposition (see Fig. 8): venous (ven) and arterial (art) plasma as well as the vascular plasma (p), endosomal (e) and interstitial (i) spaces of ten tissues. In addition to the process at the tissue level, the model incorporated the distribution of mAb via the plasma flow and the convective transport with the lymph flow from the interstitial spaces back into the plasma circulation. The rates of change of all concentrations are given by

$$\begin{aligned} V_{\rm ven} {\rm \frac{d}{dt}} C_{\rm ven} =& Q_{\rm ven}\cdot (C_{{\rm in},{\rm ven}}-C_{\rm ven}) \\ +& \sum_{\rm tis} L_{\rm tis} (1-{\rm \sigma_{\rm lymph}})C_{{\rm i},{\rm tis}} \end{aligned}$$

$$\begin{aligned} V_{\rm art} {\rm \frac{d}{dt}} C_{\rm art} = & (Q_{\rm lun} - L_{\rm lun})\cdot C_{{\rm p},{\rm lun}} - Q_{\rm art}\cdot C_{\rm art} \end{aligned}$$

(51)

$$\begin{aligned} V_{{\rm p},{\rm tis}}{\rm \frac{d}{dt}} C_{{\rm p},{\rm tis}} &= Q_{\rm tis}\cdot C_{{\rm in},{\rm tis}} - (Q_{\rm tis}-L_{\rm tis})\cdot C_{{\rm p},{\rm tis}} \\ &\quad- L_{\rm tis} (1-{\rm \sigma_{\rm vas}}) C_{{\rm p},{\rm tis}} - V_{{\rm p},{\rm tis}} k_{\rm in}\cdot C_{{\rm p},{\rm tis}} \\ &\quad + {\rm FR} Q_{{\rm out},{\rm tis}}\cdot C_{{\rm e},{\rm tis}} \end{aligned}$$

(52)

$$\begin{aligned} V_{{\rm e},{\rm tis}}{\rm \frac{d}{dt}} C_{{\rm e},{\rm tis}} = V_{{\rm p},{\rm tis}} k_{\rm in}\cdot C_{{\rm p},{\rm tis}} + V_{{\rm tis},{\rm i}} k_{\rm in}\cdot C_{{\rm tis},{\rm i}} - Q_{{\rm out},{\rm tis}} \cdot C_{{\rm e},{\rm tis}} -{\rm CLint}_{\rm e} \cdot C_{{\rm e},{\rm tis}} \end{aligned}$$

(53)

$$\begin{aligned} V_{{\rm i},{\rm tis}}{\rm \frac{d}{dt}} C_{{\rm i},{\rm tis}} = & L_{\rm tis} (1-{\rm \sigma_{\rm vas}}) C_{{\rm p},{\rm tis}}- V_{{\rm i},{\rm tis}} k_{\rm in}\cdot C_{{\rm i},{\rm tis}}\\ & - L_{\rm tis} (1-{\rm \sigma_{\rm lymph}}) C_{{\rm i},{\rm tis}}\\ & + (1-{\rm FR}) Q_{{\rm out},{\rm tis}}\cdot C_{{\rm e},{\rm tis}}. \end{aligned}$$

(54)

For all tissues except vein, artery, liver and lung, the inflowing concentration C _in was given by C _in, tis = C _art; for lung, it was $C_{{\rm in},{\rm lun}}=C_{\rm ven}$. For vein, it was

$$Q_{\rm ven} C_{{\rm in},{\rm ven}} = \sum_{{\rm tis}}\left(Q_{\rm tis}-L_{\rm tis}\right)\cdot C_{{\rm p},{\rm tis}}$$

(55)

with tis = adi, bon, hea, kid, liv, mus, ski. For liver, it was

$$\begin{aligned} Q_{\rm liv} C_{{\rm in},{\rm liv}} =& \sum_{{\rm tis}}(Q_{\rm tis}-L_{\rm tis})\cdot C_{{\rm p},{\rm tis}}+ \\ &\Big(Q_{\rm liv} - \sum_{\rm tis}Q_{\rm tis}\Big) \cdot C_{\rm art} \end{aligned}$$

(56)

with tis = gut, spl. The mAb was administered via an i.v. bolus infusion. For the vein, the initial condition of the above system of differential equations was set to

$$C_{\rm ven}(0) = \frac{{\rm dose}}{V_{\rm ven}},$$

(57)

while we set C _cmt(0) = 0 for all other compartments ’cmt’.

Fig. 8

Detailed PBPK model structure. Top structure of the PBPK model for mAbs. Organs, tissues and plasma spaces are interconnected by the plasma flow (red and blue solid arrows) and the lymphatic system (green dashed arrows). Bottom detailed organ model comprising a plasma compartment, the endosomal and the interstitial spaces. Q and L represent the plasma and lymph flow, ${\rm \sigma_{\rm vas}}$ and ${\rm \sigma_{\rm lymph}}$ denote the vascular and lymphatic reflection coefficients, k _in is the rate of uptake of mAb from the plasma or interstitial space into the endosomal space. The parameter k _out is the recycling rate constant of mAb from the endosomal space (with a fraction FR recycled into the vascular space), while fuCL_e denotes its linear clearance in the endosomal space

Lumping all (vascular) plasma spaces and tissue sub-compartments

The following reduction was justified based on time-scale arguments. To this end, we considered the generic ODE for the rate of change of the concentration C _cmt of some compartment ‘cmt’ with inflow Q _inflow and outflow Q _outflow:

$$V_{\rm cmt} {\rm \frac{d}{dt}}{C_{\rm cmt}} = Q_{\rm inflow} \cdot C_{\rm in} - Q_{\rm outflow} \cdot C_{\rm cmt}.$$

(58)

The response time τ_cmt—i.e., the time scale, on which the compartment concentration responses to changes in the inflowing concentration C _in—is given by

$$\tau_{\rm cmt} = \frac{\ln(2)}{Q_{\rm outflow}/V_{\rm cmt}}.$$

(59)

Hence, small compartments or compartments with large outflow response quickly to changes in the inflow. Of note, the inflow Q _inflow does only influence the concentration levels C _cmt and its steady state concentration, but has no impact on the response time.

In view of the systems of ODEs Eqs. (51–54), we identified three groups of compartments with different response times (supported by parameters values published in [7–10] and physiological insight):

• Fast: Arterial and venous plasma and peripheral plasma of all tissues with response times

  $$\tau_{\rm art} = \frac{\ln(2)}{Q_{\rm art}/V_{\rm art}}; \quad \tau_{\rm ven} = \frac{\ln(2)}{Q_{\rm ven}/V_{\rm ven}},$$

  and

  $$\tau_{{\rm p},{\rm tis}} = \frac{\ln(2)}{(Q_{\rm tis}-L_{\rm tis})/V_{{\rm p},{\rm tis}}}.$$

  We define τ_pla as the average of the above response times.

• Intermediate: The interstitial space of all tissues, with response times

  $$\tau_{\rm i} < \frac{\ln(2)}{(1-{\rm \sigma_{\rm lymph}})L_{\rm tis}/V_{\rm i}}.$$

  We define τ_int as the average of the above response times. Comparison to plasma response time: V _pla and V _i are roughly of the same order of magnitude (e.g. [5]), while L _tis is roughly two-orders of magnitude smaller than Q _tis, and $(1-{\rm \sigma_{\rm lymph}})=0.8$ [7]. Consequently, plasma & vascular compartments response is approximately two-orders of magnitude faster than the interstitial compartments, i.e., τ_pla ≪ τ_int. Of note, the much slower inflow corresponding to $(1-{\rm \sigma_{\rm vas}})L_{\rm tis}$ does not influence the response time, it only influences the interstitial concentration levels.

• Slow: The endosomal space of all tissues, with response times

  $$\tau_{\rm e} < \frac{\ln(2)}{(Q_{{\rm out},{\rm tis}}+{\rm CLint}_{\rm e})/V_{\rm e}} \leq \frac{\ln(2)}{Q_{{\rm out},{\rm tis}}/V_{\rm e}}.$$

  We define τ_end as the average of the above response times. According to [7], V _e is approximately two-orders of magnitude smaller than V _i, while at the same time Q _out, tis is five orders of magnitude smaller than Q _tis and therefore three orders of magnitude smaller than L _tis. Consequently, interstitial compartments response is approximately one order of magnitude faster than the endosomal compartments, i.e., τ_int < τ_end.

The above time-scale considerations suggest to lump together arterial and venous plasma and all peripheral plasma spaces, resulting in a lumped plasma compartment with total plasma volume V _pla and plasma concentration defined by

$$V_{\rm pla} \cdot C_{\rm pla} = V_{\rm art} C_{\rm art} + V_{\rm ven} C_{\rm ven} + \sum_{\rm tis} V_{{\rm p},{\rm tis}} C_{{\rm p},{\rm tis}}.$$

(60)

Moreover, due to the larger uncertainty of parameters related to the endosomal space, we decided to lump together the interstitial and endosomal space of each tissue. For easier comparison to experimental data, we also included the intracellular space with volume V _c, and defined the tissue volume by V _tis = V _i + V _e + V _c and the tissue concentration by

$$V_{\rm tis} \cdot C_{\rm tis} = V_{\rm i} \cdot C_{\rm i} + V_{\rm e} \cdot C_{\rm e} + V_{\rm c} \cdot C_{\rm c}.$$

(61)

Since the mAb—in the absence of a target—does not distribute in the intracellular space, it is C _c = 0.

We finally derived the ODEs describing the rate of change of C _pla and C _tis in the different tissues. For plasma, we obtained

$$\begin{aligned} V_{\rm pla} {\rm \frac{d}{dt}}{C_{\rm pla}} =& V_{\rm art} {\rm \frac{d}{dt}}{C_{\rm art}} + V_{\rm ven} {\rm \frac{d}{dt}}{C_{\rm ven}} + \sum_{\rm tis} V_{{\rm p},{\rm tis}} {\rm \frac{d}{dt}}{C_{{\rm p},{\rm tis}}} \\ =& \sum_{\rm tis} L_{\rm tis} (1-{\rm \sigma_{\rm lymph}})C_{{\rm i},{\rm tis}} + {\rm FR} Q_{{\rm out},{\rm tis}} C_{{\rm e},{\rm tis}} \\ & - \left( L_{\rm tis} (1-{\rm \sigma_{\rm vas}}) + V_{{\rm p},{\rm tis}} k_{\rm in} \right) C_{{\rm p},{\rm tis}}. \end{aligned}$$

We subsequently exploited $C_{\rm pla}=C_{\rm ven}=C_{\rm art}=C_{{\rm p},{\rm tis}}$ and made the following assumptions, to derive the final equation for plasma: (i) Since it is difficult to distinguish between the two-pore-related and the fluid-phase endocytotic part of the vascular extravasation, i.e., $L_{\rm tis} (1-{\rm \sigma_{\rm vas}})$ versus $V_{{\rm p},{\rm tis}} k_{\rm in}$, we only used a single term ($L_{\rm tis} (1-\sigma_{\rm tis})$) and introduced an effective lumped reflection coefficient σ_tis such that

$$L_{\rm tis} (1-\sigma_{\rm tis}) = L_{\rm tis} (1-{\rm \sigma_{\rm vas}}) + V_{{\rm p},{\rm tis}} k_{\rm in}$$

(62)

Further, (ii) since we lump all tissue sub-compartments, we assumed that $C_{\rm e}$and $C_{\rm i}$ are multiples of the lumped concentration C _tis, i.e. C _e = α C _tis and $C_{\rm i}=\beta C_{\rm tis}$. Writing moreover $Q_{{\rm out},{\rm tis}}$ as a fraction δ of the lymph flow L _tis yielded

$$\begin{aligned} {L_{\rm tis} (1-{\rm \sigma_{\rm lymph}})C_{{\rm i},{\rm tis}} + {\rm FR}\, Q_{{\rm out},{\rm tis}} C_{{\rm e},{\rm tis}} } \;=\; L_{\rm tis} \big( (1-{\rm \sigma_{\rm lymph}})\beta + {\rm FR}\, \delta \alpha \big) \cdot C_{\rm tis} \end{aligned}$$

(63)

and allowed us to define the tissue partition coefficient K _tis as

$$\frac{1}{K_{\rm tis}} = (1-{\rm \sigma_{\rm lymph}})\beta + {\rm FR} \,\delta \alpha.$$

As a consequence, we obtained the final ODE for the rate of change of the plasma concentration

$$V_{\rm pla} {\rm \frac{d}{dt}}{C_{\rm pla}} = \sum_{\rm tis} L_{\rm tis} \frac{C_{\rm tis}}{K_{\rm tis}} - L_{\rm tis} (1-\sigma_{\rm tis}) C_{\rm pla},$$

which is identical to Eq. (2). For the tissue concentration C _tis we obtained

$$\begin{aligned} V_{\rm tis} {\rm \frac{d}{dt}}{C_{\rm tis}} \;=\;& V_{\rm i} {\rm \frac{d}{dt}}{C_{\rm i}} + V_{\rm e} {\rm \frac{d}{dt}}{C_{\rm e}} + V_{\rm c} {\rm \frac{d}{dt}}{C_{\rm c}} \\ \;=\;& \left( L_{\rm tis} (1-{\rm \sigma_{\rm vas}}) + V_{{\rm p},{\rm tis}} k_{\rm in} \right) C_{{\rm p},{\rm tis}} \\ & - L_{\rm tis} (1-{\rm \sigma_{\rm lymph}})C_{{\rm i},{\rm tis}} - {\rm FR}\, Q_{{\rm out},{\rm tis}} C_{{\rm e},{\rm tis}} \\ & - {\rm CLint}_{\rm e} \cdot C_{{\rm e},{\rm tis}}. \end{aligned}$$

Defining the intrinsic tissue clearance ${\rm CLint}_{\rm tis} = {\rm CLint}_{\rm e}\cdot\alpha$ and using the same assumptions and arguments as above, we obtained

$$V_{\rm tis} {\rm \frac{d}{dt}}{C_{\rm tis}} = L_{\rm tis} (1-\sigma_{\rm tis}) C_{\rm pla} - L_{\rm tis} \frac{C_{\rm tis}}{K_{\rm tis}} - {\rm CLint}_{\rm tis} \cdot C_{\rm tis},$$

which is identical to Eq. (1). In summary, we derived our simplified PBPK model given in Eqs. (1–2) from a much more detailed PBPK model by considering time-scale separation and additional well-grounded assumptions. The resulting number of equations was reduced by a factor of approximately 6 and 3 in comparison to [7] and [10], respectively.

Derivation of the ODEs of the lumped compartments

Based on Eq. (13), we derived the ODE describing the rate of change of the lumped concentrations C _L with L = {${\rm tis}_1, \ldots, {\rm tis}_k$}. To this end, we first established the relation between the lumped concentration C _L and some tissue concentrations C _tis with ${\rm tis}\in{\rm L}$. Starting from Eq. (13), we obtained

$$\begin{aligned} V_{\rm L} \cdot C_{\rm L} =& \sum_{i=1}^k V_{{\rm tis}_i} \cdot C_{{\rm tis}_i} \\ =& \sum_{i=1}^k \left( V_{{\rm tis}_i} (1-\sigma_{{\rm tis}_i}) \widehat{K}_{{\rm tis}_i} \cdot \frac{C_{{\rm tis}_i}}{(1-\sigma_{{\rm tis}_i})\cdot \widehat{K}_{{\rm tis}_i}} \right) \cr =& \left( \sum_{i=1}^k V_{{\rm tis}_i} (1-\sigma_{{\rm tis}_i}) \widehat{K}_{{\rm tis}_i} \right) \cdot \frac{C_{\rm tis}}{(1-\sigma_{\rm tis}) \cdot\widehat{K}_{\rm tis}} \\ =& V_{\rm L} (1-\sigma_{\rm L})\cdot \widehat{K}_{\rm L} \cdot \frac{C_{\rm tis}}{(1-\sigma_{\rm tis}) \cdot\widehat{K}_{\rm tis}}, \end{aligned}$$

where we used in the third line the lumping criterion $C_{\rm tis}/((1-\sigma_{\rm tis}) \cdot\widehat{K}_{\rm tis}) = C_{{\rm tis}_i}/((1-\sigma_{{\rm tis}_i})\cdot \widehat{K}_{{\rm tis}_i})$ for ${\rm tis}\in{\rm L}$ and i = 1,…, k; and in the last line we used Eq. (14). Rearranging the above equation yielded

$$C_{\rm tis} = (1-\sigma_{\rm tis}) \widehat{K}_{\rm tis} \cdot \frac{C_{\rm L}}{(1-\sigma_{\rm L}) \widehat{K}_{\rm L}}.$$

(64)

For the plasma compartment, this specifically read

$$C_{\rm pla} = \frac{C_{\rm cen}}{(1-\sigma_{\rm cen}) \widehat{K}_{\rm cen}}.$$

For all compartments except for the central compartment, we obtained

$$\begin{aligned} V_{\rm L} {\rm \frac{d}{dt}}{C_{\rm L}} \;=\;& \sum_{{\rm tis}\in{\rm L}} L_{\rm tis} \cdot \left( (1-\sigma_{\rm tis}) C_{\rm pla} - \frac{C_{\rm tis}}{\widehat{K}_{\rm tis}} \right) \\ \;=\;& \sum_{{\rm tis}\in{\rm L}} L_{\rm tis} (1-\sigma_{\rm tis}) \left(C_{\rm pla} - \frac{C_{\rm tis}}{(1-\sigma_{\rm tis})\widehat{K}_{\rm tis}} \right) \\ \;=\;& \sum_{{\rm tis}\in{\rm L}} L_{\rm tis} (1-\sigma_{\rm tis}) \left(C_{\rm pla} - \frac{C_{\rm L}}{(1-\sigma_{\rm L})\widehat{K}_{\rm L}} \right) \\ \;=\;& L_{\rm L}(1-\sigma_{\rm L}) \left( C_{\rm pla} - \frac{C_{\rm L}}{(1-\sigma_{\rm L})\widehat{K}_{\rm L}} \right). \end{aligned}$$

where we exploited Eq. (64) in the third line. Thus

$$\begin{aligned} V_{\rm L} {\rm \frac{d}{dt}}{C_{\rm L}} \;=\;& L_{\rm L} \left((1-\sigma_{\rm L}) C_{\rm pla} - \frac{C_{\rm L}}{\widehat{K}_{\rm L}} \right) \\ \;=\;& L_{\rm L} \left((1-\sigma_{\rm L}) C_{\rm pla} - \frac{C_{\rm L}}{K_{\rm L}} \right) - {\rm CLint}_{\rm L} C_{\rm L}. \end{aligned}$$

For the central compartment, we obtained

$$\begin{aligned} V_{\rm cen} {\rm \frac{d}{dt}}{C_{\rm cen}}&= \sum_{{\rm tis}} L_{\rm tis} \left( \frac{C_{\rm tis}}{K_{\rm tis}} - (1-\sigma_{\rm tis}) C_{\rm pla} \right) +{\ldots} \\ &\quad + \sum_{{\rm tis}\in{\rm cen}} L_{\rm tis} \left((1-\sigma_{\rm tis})C_{\rm pla} - \frac{C_{\rm tis}}{\widehat{K}_{\rm tis}} \right)\\ &= \sum_{{\rm tis}\notin{\rm cen}} L_{\rm tis} (1-\sigma_{\rm tis})\left( \frac{C_{\rm tis}}{(1-\sigma_{\rm tis})K_{\rm tis}} - C_{\rm pla} \right) +{\ldots} \\ &\quad+ \sum_{{\rm tis}\in{\rm cen}} L_{\rm tis} \left( \frac{C_{\rm tis}}{\widehat{K}_{\rm tis}} - (1-\sigma_{\rm tis})C_{\rm pla} \right) \\ &\quad - E_{\rm tis} L_{\rm tis} \frac{C_{\rm tis}}{\widehat{K}_{\rm tis}} - \sum_{{\rm tis}\in{\rm cen}} L_{\rm tis} \cdot \left( \frac{C_{\rm tis}}{\widehat{K}_{\rm tis}} - (1-\sigma_{\rm tis}) C_{\rm pla} \right) \\ &= \sum_{{\rm L}} L_{\rm L} (1-\sigma_{\rm L})\left( \frac{C_{\rm L}}{(1-\sigma_{\rm L})\widehat{K}_{\rm L}} - C_{\rm pla} \right) \\ &\quad - E_{\rm cen} L_{\rm cen} (1-\sigma_{\rm cen}) \cdot C_{\rm pla} \\ &= \sum_{{\rm L}} L_{\rm L} \left( \frac{C_{\rm L}}{\widehat{K}_{\rm L}} - (1-\sigma_{\rm L})C_{\rm pla} \right) -{\rm CLpla}_{\rm cen} \cdot C_{\rm pla}\\ &= L_{\rm cen} \Big( C_{{\rm in},{\rm L}} - (1-\sigma_{\rm cen})C_{\rm pla} \Big) - {\rm CLpla}_{\rm cen} \cdot C_{\rm pla}, \end{aligned}$$

where we exploited in particular Eqs. (12) and (16). These equations are the foundation for the derivation of lumped compartment models in the next section.